A DataSet About College Majors

What kind of Data am i researching about and why?

My name is Max Juarez and i'm currently enrolled in Lehman College. I'm currently pursuing a degree in Computer Science while also trying to minor in mathematics. Since the day i had first enrolled in my very first class, i am proud to say that i have debated on pursuing in a different degree rather than trying to major in Computer Science thus the DataSet about College Majors piqued my interest.

Why did it piqued my interest?

I've always thought that technology will soon evolve to something greater that might eventually shape the whole world into something magnificent so i wanted to see whether or not Computer Science had a lot of enrolls. I was also interested in other majors that i wanted to try out other than Computer Science.

This dataset contains a few headers with a description as to what they are meant to show (purposes)

The headers are as follow:

1. Major_code - Major Code, FO1DP in ACS PUMS
2. Major - Major description
3. Major_category - Category of major from Carnevale et al
4. Total- Total number of people with major
5. Employed - Number of employed (ESR == 1 or 2)
6. Employed_full_time_year_round - Employed at least 50 weeks (WKW ==1 ) and at least 35 hours (WKHP >= 35)
7. Unemployed - Number of unemployed (ESR ==3 )
8. Unemployment_rate - Unemployed / (Unemployed + Employed)
9. Median - Median earnings of full-time, year-round workers
10. P25th - 25th percentile of earnigns
11. P75th - 75th percentile of earnings

Unanswered questions i came up with?

What are the top 10 Majors with the most people enrolled in percentage and why do you (i) think these majors are the most popular?

The major with the most Employed?

The Major with the most unemployed?

Which of the majors have the least unemployment rate?

What is "Total"?

The total is defined as the amount of people that are majoring in a specific major, such as Computer Science, Nursing, Pharmacology, Geological and Geophysical Engineering, and so on. The total amount of students majoring in a specific kind of major is extremely valuable to determine the most popular type of degree and the least popular type of degree. The mean, standard deviation, skewness and kurtosis are:

Mean: 230256.6
Standard Deviation: 422068.5
Skewness: 3.591402
Kurtosis: 15.98407

BoxPlot and Histogram of the data "Total"

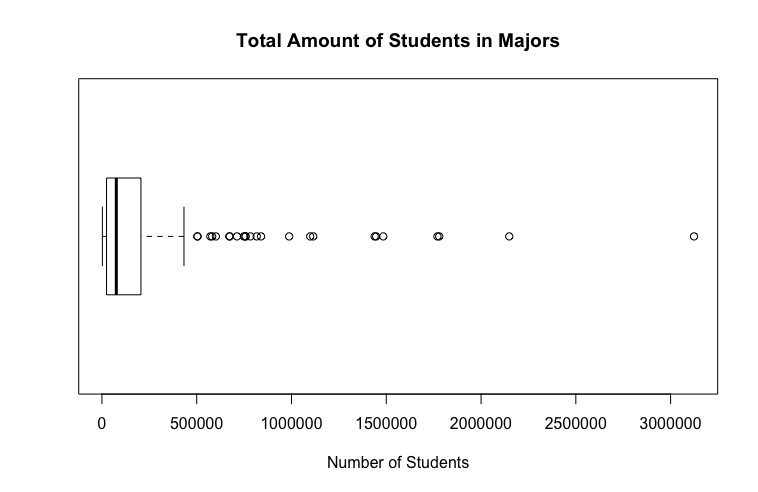
The boxplot used to plot the column Total of all-ages.csv is essential to understand the amount of students who ended up with pursing a major. It appears as if the boxplot was the one and only graph that truly captured the data's purpose. One can easily find the outliers, datum detached from the rest of the data that looked inconsistent and it appears that the graph captured 24 outliers, data that exceeded an amount that other data did not. These 24 outliers were the top 24 majors that were popular among other majors.

The data's histogram has a skewness of 3.591402 and a kurtosis of 15.98. The kurtosis's value appears to categorize the data as a platykurtic and a positive skewness which let me to believe that the data is slightly skewed to the right. Although, it appears that the graph has a random distribution. My assumption is that the histogram didn't help as much as i thought it would've had.

Computing a confidence interval for the "Total" # 1:

Knowing that the mean of the data "Total" is mean = 230256.6, the standard deviation = 422068.5, and the dataset has a length of n = 173. We can compute the margin of error by adding/subtracting the mean from the confidence level times the standard deviation over the square root of n (230256.6 ± 1.959964 * 422068.5/sqrt(173)) which gives us the range where the true mean lands on: [167362.8, 293150.4].